Inference via Stan for the Mean and Variance of a Gaussian ("Normal") Population with Weakly Informative and Fiducial Priors

Preamble

Attenion Conservation Notice: I implement the now-standard Bayesian procedure for estimating a Gaussian mean and variance with weakly informative priors using Stan and make some connections to confidence distributions and fiducial inference. But without any of the details for this to make sense for a newcomer. For the former material, you are better served by page 73 of A First Course in Bayesian Statistical Methods by Peter Hoff or page 67 of Bayesian Data Analysis. For the latter material, by Confidence, Likelihood, Probability by Tore Schweder and Nils Lid Hjort.

Consider simultaneously estimating the population mean and population variance of a Gaussian (“Normal”) population \(N(\mu, \sigma^{2})\) where both the mean and variance are unknown. This is the textbook case of statistical inference, which in the Frequentist case is solved by using the sample mean and sample variance of a random sample \(X_{1}, X_{2}, \ldots, X_{n}\).

But let’s solve it using a Bayesian procedure with a weakly informative prior for the population mean and population variance. We’ll focus on the precision \(1 / \sigma^{2}\) rather than the variance \(\sigma^{2}\) since the precision’s conjugate prior is a Gamma distribution, and it allows us to demonstrate some features of Stan. We will assume the prior factors as \(p(\mu, 1/\sigma^{2}) = p(1 / \sigma^{2}) p(\mu \mid 1/\sigma^{2})\), and take the following marginal and conditional distributions¹: \[ \begin{aligned} 1/\sigma^{2} &\sim \text{Gamma}(\nu_{0}/2, \sigma_{0}^{2} \nu_{0}/2) \\ \mu \mid \sigma^{2} & \sim N(\mu_{0}, \sigma^{2}/ \kappa_{0}). \end{aligned} \] That is, the precision follows a Gamma distribution parametrized by \(\nu_{0}\) – which can be thought of as the sample size for the prior estimate of the variance \(\sigma_{0}^{2}\) – and the conditional distribution of the mean follows a Gaussian distribution parametrized by \(\kappa_{0}\) – which can be thought of as the sample size for the prior estimate \(\mu_{0}\) of the mean.

Stan Implementation

One can write down the posterior distribution \(p(\mu, 1 / \sigma^{2} \mid x_{1}^{n})\) given a sample \(x_{1}^{n}\) from a Gaussian population, but let’s be lazy and use Stan to do all of the heavy lifting, and then check our answer using the theoretical result.

data {
  int N; // the sample size
  vector[N] x; // the data
  real mu0; // mean for prior on mu
  real kappa0; // sample size for prior on mu
  real sigma0; // prior value for sigma
  real nu0; // sample size for prior on sigma^2
}

parameters {
  real mu; // the mean
  real<lower=0> prec; // the precision, 1 / variance
}

transformed parameters{
  real<lower=0> sigma;
  
  sigma = 1/sqrt(prec);
}

model {
  prec ~ gamma(nu0/2, nu0/2*square(sigma0)); // prior for the precision
  mu ~ normal(mu0, sigma/sqrt(kappa0)); // conditional prior for the mean
  
  x ~ normal(mu, sigma); // likelihood for the data
}

As with any Stan model, we set up the data in the first block, the parameters in the second, and the model in the final block. We include a transformation of the precision back to the standard deviation for ease later. We could have also done this all in terms of the variance by using the inverse-Gamma distribution, but this way we get to practice making the transformation.

MCMC Goes Brr

We run the model with cmdstanr.

library(cmdstanr)

## Warning: package 'cmdstanr' was built under R version 4.0.5

options(mc.cores = 4)

set.seed(314)

N <- 3

x <- rnorm(N, mean = 0, sd = 1)

mu0  <- 0 # prior mean for mu
kappa0 <- 1 # prior sample size for mu

sigma0 <- 1 # prior mean for sigma
nu0 <- 1 # prior sample size for sigma

data.for.stan <- list(N = N, 
                      x = x,
                      mu0 = mu0,
                      kappa0 = kappa0, 
                      sigma0 = sigma0,
                      nu0 = nu0
                      )

mod <- cmdstanr::cmdstan_model('gaussian-model-with-conditional-prior.stan')

num.samples <- 50000 # Number of HMC samples to draw per-core, so total samples is 4*50000

fit <- mod$sample(data.for.stan, chains = 4, iter_sampling = num.samples,
                  refresh = num.samples/2)

## Running MCMC with 4 parallel chains...
## 
## Chain 3 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 3 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 4 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 4 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 1 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 1 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 2 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 2 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 1 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 2 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 3 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 4 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 1 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 1 finished in 0.9 seconds.
## Chain 4 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 4 finished in 1.0 seconds.
## Chain 2 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 3 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 2 finished in 1.0 seconds.
## Chain 3 finished in 1.0 seconds.
## 
## All 4 chains finished successfully.
## Mean chain execution time: 1.0 seconds.
## Total execution time: 1.3 seconds.

sim <- fit$draws(format = 'df')

Posterior Parameters

Because the prior we chose is conjugate to the Gaussian model, the posterior distributions for the mean and precision are also Normal and Gamma, namely, \[ \begin{aligned} 1 / \sigma^{2} \mid X_{1}^{n} &\sim \mathrm{Gamma}(\nu_{n}/2, \sigma_{n}^{2} \nu_{n}/2)\\ \mu \mid X_{1}^{n}, 1/\sigma^{2} &\sim N(\mu_{n}, \sigma^{2} / \kappa_{n}) \end{aligned} \] where the updated parameters are given by \[ \begin{aligned} \mu_{n} &= \frac{\kappa_{0} \mu_{0} + n \bar{x}}{\kappa_{0} + n} \\ \kappa_{n} &= \kappa_{0} + n \\ \sigma_{n}^{2} &= \frac{\nu_{0} \sigma_{0}^{2} + (n - 1)s^{2} + \frac{\kappa_{0}n}{\kappa_{0} + n} (\bar{x} - \mu_{0})^{2} }{\nu_{0} + n} \\ \nu_{n} &= \nu_{0} + n \end{aligned} \] Computing these:

kappaN <- kappa0 + N

nuN <- nu0 + N

muN <- kappa0*mu0/(kappa0 + N)  + N*mean(x)/(kappa0 + N)

sigmaN2 <- (nu0*sigma0^2 + (N - 1)*var(x) + kappa0*N / (kappa0 + N) * (mean(x) - mu0)^2)/nuN

Comparison of Simulated Posterior Distributions to Exact Posterior Distributions

Comparing the exact posterior mean to the MCMC posterior mean,

muN

## [1] -0.3484249

mean(sim$mu)

## [1] -0.3524828

we get pretty good agreement, as expected.

Because we know that the posterior distribution of the precision follows a Gamma distribution, we can fit the Gamma distribution via MLE to the posterior draws from MCMC and check that that parameters match:

gamma.fit <- MASS::fitdistr(sim$prec, 'gamma')

hist(sim$prec, breaks = 'FD', freq = FALSE)

curve(dgamma(x, gamma.fit$estimate['shape'], gamma.fit$estimate['rate']), col = 'cyan', add = TRUE)

The fit is clearly very good, and the MLEs match the shape and rate:

gamma.fit

##       shape         rate    
##   1.986139325   1.689701902 
##  (0.005830245) (0.005638236)

nuN/2

## [1] 2

nuN/2*sigmaN2

## [1] 1.698458

The marginal, rather than conditional, posterior distribution of the mean follows a generalized \(t\)-distribution such that \[ \frac{\mu - \mu_{n}}{\sigma_{n}/\sqrt{\kappa_{n}}} \sim t(\nu_{n}) \]

tstat.bayesian <- (sim$mu - muN)/sqrt(sigmaN2 / kappaN)

t.fit.bayesian <- MASS::fitdistr(tstat.bayesian, 't')

hist(tstat.bayesian, breaks = 'FD', freq = FALSE)

curve(dt(x, t.fit.bayesian$estimate[3]), add = TRUE, col = 'cyan', n = 2001)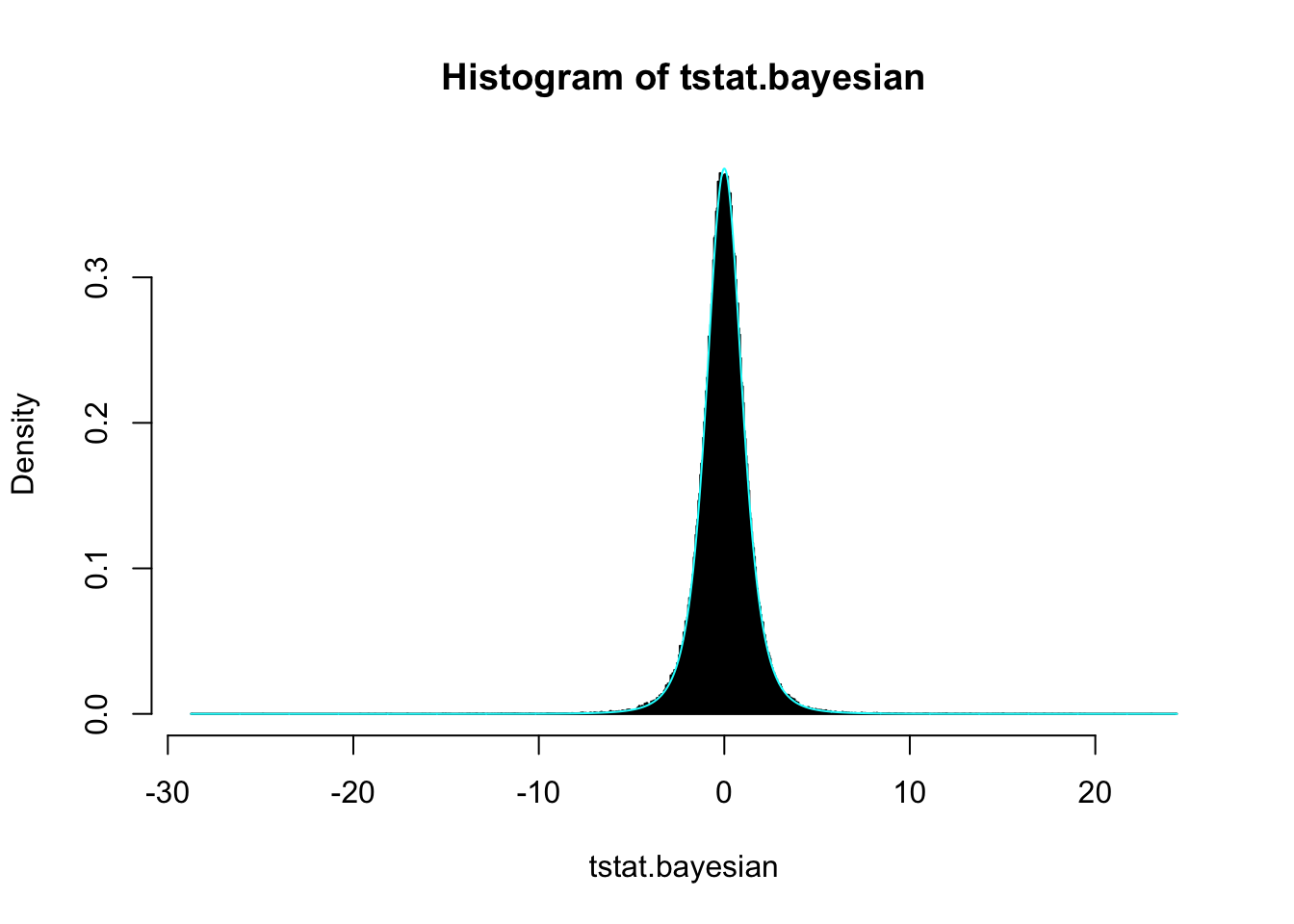

t.fit.bayesian

##         m              s              df     
##   -0.004202771    0.997067217    3.957782156 
##  ( 0.002641799) ( 0.002778722) ( 0.036179732)

nuN

## [1] 4

Alternatively, fitting the posterior distribution for \(\mu\) directly

t.fit <- MASS::fitdistr(sim$mu, 't')

t.fit

##         m              s              df     
##   -0.350361520    0.459417269    3.957812556 
##  ( 0.001217257) ( 0.001280338) ( 0.036180346)

muN

## [1] -0.3484249

sqrt(sigmaN2/kappaN)

## [1] 0.4607681

nuN

## [1] 4

we see that we recover the correct parameters from the MCMC samples.

Fiducial Distribution

Ronald Fisher determined that the fiducial distribution for \(\mu\) in the Gaussian model with unknown mean and variance also follows a generalized \(t\)-distribution.

One might hope that we could mimic the fiducial distribution in Stan by taking an approximately noninformative prior on \(\mu\) and \(1 / \sigma^{2}\) by setting \(\kappa_{n}\) and \(\nu_{n}\) (the “sample sizes” for the priors) to small positive values. This, however, does not work, and the “appropriate,” in the sense that it recovers the fiducial distribution, approach is to take \[ \begin{aligned} p(\mu) &= 1 \\ p(\sigma^{2}) &= 1/\sigma^{2}. \end{aligned} \]

This gives us the following model in Stan:

data {
  int N; // sample size
  vector[N] x; // data
}

parameters {
  real mu;
  real<lower=0> sigma2;
}

model {
  // No prior needed for mu since log(1) = 0
  target += -log(sigma2); // log(1 / sigma^2) = - log(sigma^2)
  
  x ~ normal(mu, sqrt(sigma2));
}

data.for.stan <- list(N = N, 
                      x = x)

mod.fiducial <- cmdstanr::cmdstan_model('gaussian-model-with-fiducial-prior.stan')

fit.fiducial <- mod.fiducial$sample(data.for.stan, chains = 4, iter_sampling = num.samples,
                  refresh = num.samples/2)

## Running MCMC with 4 parallel chains...
## 
## Chain 1 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 2 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 3 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 3 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 4 Iteration:     1 / 51000 [  0%]  (Warmup) 
## Chain 4 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 1 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 2 Iteration:  1001 / 51000 [  1%]  (Sampling) 
## Chain 1 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 2 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 3 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 4 Iteration: 26000 / 51000 [ 50%]  (Sampling) 
## Chain 1 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 1 finished in 0.8 seconds.
## Chain 2 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 3 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 4 Iteration: 51000 / 51000 [100%]  (Sampling) 
## Chain 2 finished in 0.9 seconds.
## Chain 3 finished in 0.9 seconds.
## Chain 4 finished in 0.9 seconds.
## 
## All 4 chains finished successfully.
## Mean chain execution time: 0.9 seconds.
## Total execution time: 1.1 seconds.

## 
## Warning: 2 of 200000 (0.0%) transitions ended with a divergence.
## This may indicate insufficient exploration of the posterior distribution.
## Possible remedies include: 
##   * Increasing adapt_delta closer to 1 (default is 0.8) 
##   * Reparameterizing the model (e.g. using a non-centered parameterization)
##   * Using informative or weakly informative prior distributions

sim.fiducial <- fit.fiducial$draws(format = 'df')

library(clp)

fd.mu <- clp::t_test.conf(x, plot = FALSE)

hist(sim.fiducial$mu, breaks = 'FD', freq = FALSE, xlim = c(-10, 10))
curve(fd.mu$dconf(x), add = TRUE, col = 'cyan', n = 2001)

Alternatively, check that \(\mu\) follows a generalized \(t\)-distribution such that \[ \frac{\mu - \bar{x}}{s/\sqrt{n}} \sim t(n - 1). \]

t.fit.fiducial <- MASS::fitdistr(sim.fiducial$mu, 't')

t.fit.fiducial

##         m             s            df     
##   -0.46494897    0.60769679    1.95677249 
##  ( 0.00176083) ( 0.00190689) ( 0.01093374)

mean(x)

## [1] -0.4645666

sd(x)/sqrt(N)

## [1] 0.6103344

N - 1 

## [1] 2

Again, we see that the posterior distribution matches the generalized \(t\).