Homework 4

Chapter 2

Repeat your analysis from Homework 3 for the following 4 problems:

Problem 2.4ab
Problem 2.6ac
Problem 2.27c
Problem 2.30ab

using both SLRGN-based (as you did in Homework 3) and bootstrap-based inferential statistics.

Directions

Use \(B = 5000\) bootstrap samples.
For a problem that asks for a confidence interval, compute the confidence interval and the confidence curve under both the SLRGN and bootstrap models.
Comment on the difference (or not) in your conclusions using the SLRGN versus bootstrap models.
Refer back to your diagnostic plots for these data sets from Homework 2, and comment on whether the SLRGN- or bootstrap-based inferential statistics are more appropriate for each data set.

Hint: You can add a new confidence curve to a previously plotted confidence curve by passing the argument add = TRUE to the new call to plot.confcurve.

Additional Problems

Duality Between Confidence Intervals and Hypothesis Testing

We wish to test, assuming the SLRGN model, the following hypothesis: \[ \begin{array}{ll} H_{0} : & \beta_{1} = \beta_{1}^{(0)} \\ H_{1} : & \beta_{1} \neq \beta_{1}^{(0)} \end{array}\] at significance level \(\alpha\).

Test Statistic Method:
1. Determine an appropriate test statistic for this hypothesis test.
2. Determine the rejection region for the appropriate test statistic for this hypothesis test at the significance level \(\alpha\).
Confidence Interval Method:
1. Determine the confidence interval that can be used to test this hypothesis.
2. Determine the condition for rejecting the null hypothesis using this confidence interval at the significance level \(\alpha\).
Show that the intervals of values of \(b_{1}\) for which the Test Statistic Method rejects the null hypothesis are equivalent to the intervals of values for which the Confidence Interval Method rejects the null hypothesis.
- Hint: For each of the two methods, write the intervals of values for which the null hypothesis is rejected as inequalities involving \(\beta_{1}^{(0)}\) and \(b_{1}\). Then show that the inequalities for each method specify the same intervals of values for \(b_{1}\).

Good Odds

The odds ratio \(\rho\) is a quantity used in medical research to compare binary outcomes under two different treatments. An odds ratio of 1 indicates that there is no difference between the two treatments.

A medical researcher has constructed a confidence curve to estimate the odds ratio between two treatments for some disease. The confidence curve from her sample data is given below.

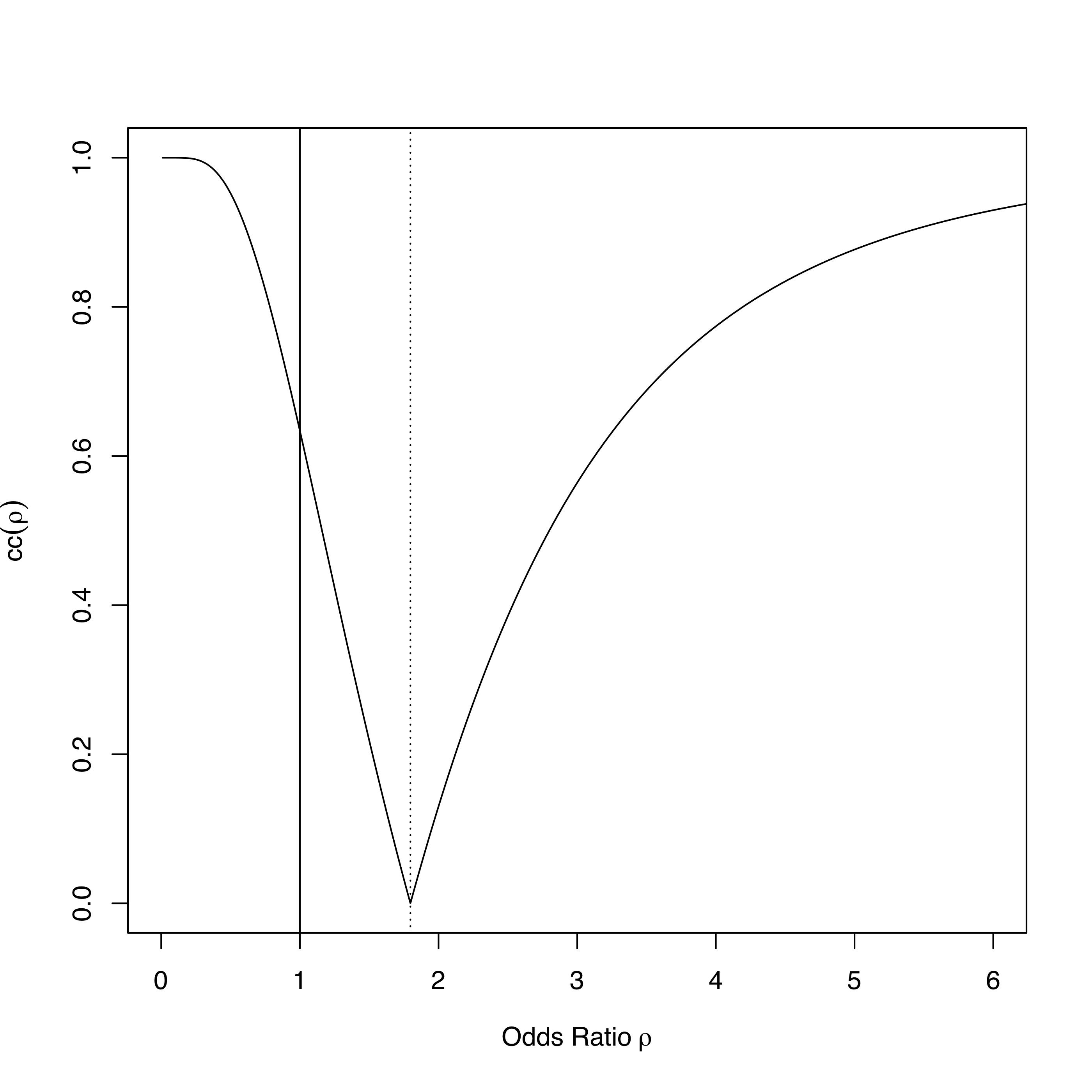
What is the 80% confidence interval for the odds ratio?
What is the \(P\)-value associated with a two-sided hypothesis test of no difference between the two treatments?

The Lazy Scientist

A scientist tests the hypothesis \[ \begin{array}{ll} H_{0} : & \beta_{1} = 0 \\ H_{1} : & \beta_{1} \neq 0 \end{array}\] using a SLRGN-based \(P\)-value. He reports the following sample statistics \[ \begin{aligned} n &= 101 \\ b_{1} &= 0.5 \\ s_{X} &= 2 \\ P &= 0.0013 \end{aligned}\] Suppose you want to know the estimate of the variance of the noise in the SLRGN model, which the scientist was too lazy to report.

What is the value of \(\widehat{\sigma_{\epsilon}^{2}}\) implied by the reported statistics?
Can you still recover the estimate of the noise variance if he had tested \[ \begin{array}{ll} H_{0} : & \beta_{1} = 2 \\ H_{1} : & \beta_{1} \neq 2 \end{array}\] instead?